"כלל 72", יאפשר לך לחשב בקלות ובמהירות, כמה שנים יידרשו, על מנת להכפיל סכום נתון, בהתאם לתשואה שתקבל בהשקעת הסכום הזה, בריבית דריבית.
איך מבצעים את החישוב עפ"י "כלל 72"?
מחלקים את המספר 72, בתשואה השנתית הנתונה.
התוצאה שתתקבל מהחלוקה הזו, הינה מספר השנים שיידרשו על מנת להכפיל את סכום ההשקעה בתשואה הנתונה, בריבית דריבית.
לדוגמא:
אם התשואה השנתית היא 6% אחוז – כמה זמן יידרש על מנת להכפיל את סכום ההשקעה?
הנה החישוב:
12 = 6 / 72
כלומר, יידרשו לי 12 שנים על מנת להכפיל את סכום ההשקעה, בתשואה של 6% בשנה, בריבית דריבית.
דוגמא נוספת:
כמה זמן ייקח להכפיל סכום נתון, בתשואה של 9% לשנה?
הנה החישוב:
8 = 9 / 72
כלומר, יידרשו לי 8 שנים על מנת להכפיל סכום נתון בתשואה של 9% לשנה, בריבית דריבית.
האם ניתן לבצע את החישוב גם בכיוון ההפוך?
כמובן!
אם תחלק 72 במספר השנים הדרוש להכפלה – התשובה שתתקבל היא התשואה שעליך להשיג על ההשקעה שלך.
לדוגמא:
נניח שאתה מעוניין להכפיל סכום מסוים בתוך 7 שנים. לאיזה תשואה תזדקק?
התשובה: כ 10% בשנה.
הנה החישוב:
10.28 = 7 / 72
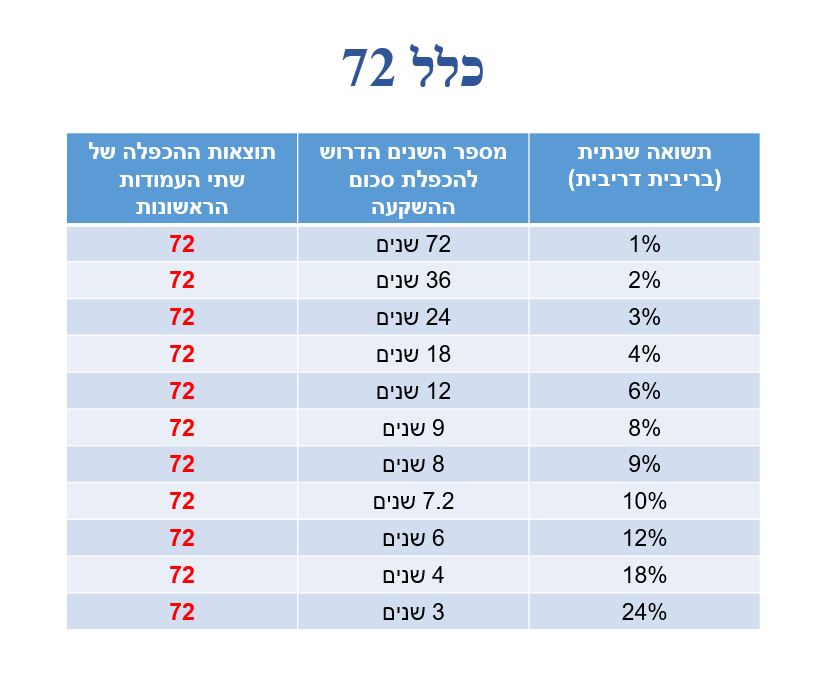
הנה טבלה המציגה ערכים נפוצים של "כלל 72":
בשביל מה צריך בכלל את "כלל 72"?
הכלל הזה, שימושי מאוד לכל מי שעוסק בהשקעות, וכדאי לזכור אותו.
למה?
כי כסף הוא משחק של הכפלות!
הדרך המהירה ביותר להגיע ליעד כספי כלשהו, היא בהכפלות, לדוגמא:
64 = 2 * 2 * 2 * 2 * 2 * 2
להבדיל מחיבור, לדוגמא:
12 = 2 + 2 + 2 + 2 + 2 + 2
לכן, כל משקיע משתדל למקסם את הונו, באמצעות הכפלת ההון שברשותו במהירות האפשרית, וחזרה על הפעולה שוב ושוב.
מה הבעיה להכפיל ב 2 שוב ושוב?
אין בעיה להכפיל ב 2 שוב ושוב…
הבעיה היא, שברוב המקרים, התשואה השנתית נמוכה מ 100% לשנה.
תשואה שנתית סבירה ומקובלת יותר היא: 4%, 6%, 8% בשנה וכו'.
לכן, יידרשו למשקיע מספר שנים על מנת להכפיל את השקעתו.
משך הזמן שיידרש למשקיע על מנת להכפיל את השקעתו – תלוי בתשואה השנתית שהמשקיע משיג על השקעתו.
ככל שהתשואה השנתית גבוהה יותר, יידרש פחות זמן להכפלת הסכום, ולהפך.
בנקודה הזו בדיוק, בא לעזרתנו "כלל 72", ומאפשר לנו לחשב בקלות ובמהירות, כמה זמן יידרש להכפיל סכום כלשהו, בהתאם לתשואה שהמשקיע משיג.
הנה מספר דוגמאות שכיחות, למצבים בהם ניתן ליישם את "כלל 72"?
- תשואה שכיחה מהשכרת דירה להשקעה, הינה 3% לשנה.
כמה זמן ייקח למשקיע להכפיל את שווי הדירה, בהנחה שהתשואה תתקבל בריבית דריבית?
תשובה: 24 שנים.
הנה החישוב:
24 = 3 / 72
- התשואה ממוצעת ארוכת טווח בשוק ההון הינה 7% לשנה.
בתוך כמה שנים יכפיל המשקיע את השקעתו?
תשובה: בתוך כ 10 שנים.
הנה החישוב:
10.28 = 7 / 72
- בהנחה שאתה מסוגל להשיג תשואה של 12% לשנה, בריבית דריבית על ההשקעה שלך – בתוך כמה שנים תכפיל את ההשקעה?
תשובה: בתוך 6 שנים.
הנה החישוב:
6 = 12 / 72
הערה לגבי "ריבית דריבית" ב"כלל 72":
החישוב עפ"י "כלל 72", רלוונטי אך ורק למצבים בהם התשואה המתקבלת על ההשקעה הינה בריבית דריבית.
לדוגמא:
נניח שהשקעת 100,000 ש"ח בריבית רגילה בשיעור של 10% בשנה.
במקרה כזה, בכל שנה, התשואה בשיעור 10% – תהיה סכום קבוע בסך 10,000 ש"ח.
כלומר, יידרשו לך 10 שנים על מנת להכפיל את ההשקעה שלך מ 100 ל 200 אלף ש"ח.
הנה החישוב:
100,000 = 10,000 * 10
לעומת זאת, אם התשואה שלך תתקבל בריבית דריבית, הרי שבכל שנה, תקבל ריבית בסכום גבוה יותר מהשנה הקודמת:
בשנה הראשונה, הריבית תהיה בסך 10,000 ש"ח, שהם 10% מתוך 100,000 ש"ח.
בשנה השנייה, הריבית תהיה בסך 11,000 ש"ח, כי מדובר בריבית דריבית, כלומר, 10% על סך של 110,000 ש"ח.
בשנה השלישית, הריבית תהיה בסך 12,100 ש"ח, כי מדובר בריבית דריבית, כלומר, 10% על סך של 121,000 ש"ח.
בשנה הרביעית, הריבית תהיה בסך 13,310 ש"ח, כי מדובר בריבית דריבית, כלומר, 10% על סך של 133,100 ש"ח.
וכך הלאה, עד שיצטברו 200,000 ש"ח.
כפי שאתה רואה, הכפלת הסכום באמצעות ריבית דריבית, תהיה מהירה יותר בהשוואה לריבית רגילה, ותימשך עפ"י "כלל 72" – 7.2 שנים בלבד.
הנה החישוב:
7.2 = 10 / 72
והנה הנוסחה לבדיקה, שסכום ההשקעה אכן מוכפל בתוך 7.2 שנים:
198,622 = 7.2 ^ 1.1 * 100,000
עד כמה "כלל 72" מדויק?
כפי שראית בדוגמא שלעיל, עפ"י "כלל 72", הכפלת ההון בתשואה של 10% בשנה, בריבית דריבית, תימשך 7.2 שנים.
יחד עם זאת, מחישוב מדויק שביצענו באמצעות המחשב, גילינו שבתוך 7.2 שנים, נגיע "רק" ל 198,622 ש"ח, ולא ל 200,000 ש"ח "עגול".
באופן דומה, אם תבצע חישוב מדויק בתשואה שנתית של 6% לשנה, הרי שעפ"י כלל 72, תזדקק ל 12 שנים על מנת להכפיל את סכום ההשקעה.
הנה החישוב:
12 = 6 / 72
אולם חישוב מדויק שנבצע, יוביל לתוצאה הבאה:
201,220 = 12 ^ 1.06 * 100,000
כלומר, גם במקרה הזה, נגיע לסכום קרוב, 201,220, אבל לא לסכום "עגול" של 200,000 ש"ח.
אם תבצע בדיקה דומה גם לגבי יתר הערכים המתקבלים עפ"י "כלל 72" – תגלה שוני קל בהשוואה בין התוצאות המתקבלות משימוש "בכלל 72", לתוצאות שמתקבלות בבדיקה מדויקת באמצעות המחשב.
לסיכום:
"כלל 72", לא נותן תשובה מדויקת "על הנקודה", ואינו יכול להוות תחליף לחישוב מדויק באמצעות מחשב, כאשר חישוב מדויק אכן נדרש.
יחד עם זאת, "כלל 72" מספק לנו תשובה מספיק טובה, ולכן הוא כל כך שימושי לכל מי שעוסק בהשקעות.
אהבת את המאמר?
חושב שהמאמר יכול לעזור למישהו?
אשמח אם תשתף אותו עם חבר…
אזהרה
קריאת המאמר כפופה לתנאי השימוש באתר.
הכותב אינו יועץ השקעות ואינו יועץ פנסיוני.
כל האמור במאמר הינו דעתו האישית בלבד של הכותב, שהועלתה על הכתב למטרות בידוריות ו/או על מנת להסב את תשומת לבו של הקורא.
אין לראות באמור התחייבות להשגת תשואות ו/או רווח כלשהו.
המאמר הינו כללי מאוד, לא בהכרח מדויק, ואינו מתיימר למצות את החוקים ו/או הדין הרלוונטיים באילו מהנושאים המוזכרים בו.
הכותב לא מתחייב לתקן ו/או לעדכן את המאמר, אם וככל שיחולו שינויים ו/או עדכונים במידע ו/או בחוקים הרלוונטיים לנושאים שעלו במאמר.
אין לראות במאמר ייעוץ ו/או שיווק השקעות מכל סוג שהוא, והוא אינו תחליף לייעוץ מקצועי אישי מאת בעל מקצוע ו/או הכשרה ו/או רישיון מתאימים, המתחשב בנתוניו ו/או בצרכיו האישיים של כל אדם.
יש להפעיל שיקול דעת. כל המסתמך על המאמר בביצוע אילו מהפעולות שהוזכרו בו – עושה זאת על דעתו ועל אחריותו בלבד.